Pre-Calculating Wire-Feed Speed, Travel Speed and Voltage
It is possible for manufacturers that are welding with solid wire or flux-cored wire to calculate the starting wire-feed speed and travel speed? These calculations will get you close, but some tweaking may have to be done to achieve your desired weld.
Posted: December 1, 2010
A shop would like to decrease the development time for new MIG welds. Is there a way to pre-calculate wire-feed speed, travel speed and voltage, to get them close before they strike the first weld?
Yes, it is possible to calculate starting wire-feed speed and travel speed. This is a very common question from manufacturers welding with solid wire or flux-cored wire. Most welding professionals know the wire-feed speed (WFS), where a process runs well based on their experience, or can quickly get WFS from the manufacturer’s recommended procedures.
However, determining how fast to travel for a particular size weld bead ends up being an iterative, time-consuming process. By understanding a few concepts and doing some math with a few simple formulas, we can determine at least a good starting point for a welding procedure that produces the desired weld.
DEPOSITION RATE
It is essential to recall that Deposition Rate is directly proportional to the speed at which a particular wire diameter emerges from a welding gun during welding. Deposition rate has nothing to do with how fast the gun is traveling, nor the voltage setting on the machine. Deposition rate is simply a measure of how many pounds of wire come from the welding gun in a certain amount of time, typically measured in lb/hr.
If wire-feed speed increases, deposition rate increases. We also understand that if we maintain the wire-feed speed and change to a larger diameter wire, deposition rate will increase as well. Armed with this understanding, calculating deposition rate ends up being a very powerful exercise that gives you a number that can be used to calculate key welding parameters. Let’s look at the formula and an example:
Deposition Rate Calculation
Deposition rate (lb/hr) = 13.1 × (Wire diameter)2 × (Wire-feed speed) × (Efficiency)
— Wire diameter in inches (in)
— Wire-feed speed in inches per minute (ipm)
— Efficiency (1.0 for solid wire, 0.85 for cored wire)
— This calculation is for steel only
— e.g.: Wire diameter = 0.045 in (1.2 mm) solid wire, WFS = 300 ipm
Deposition rate = 13.1 × (0.045)2 × (300) × (1.0) = 7.96 lb/hr
Calculating Travel Speed With Deposition Rate
Knowing the deposition rate, we can calculate the travel speed in inches per minute (ipm) for a particular weld. Let’s say we want to make a 3/8 in steel fillet weld (assume 10 percent reinforcement or 0.4125 in leg) using 0.045 in solid wire at 300 ipm, the weight of weld metal per foot can be calculated by multiplying the density of steel (0.283 lb/in3) by the volume of weld metal per foot as follows:
Weld Weight Per Foot Calculation
Volume of weld metal/ft = 1/2 × b × h × 12 in = 1/2 × 0.4125 in × 0.4125 in × 12 in = 1.02 in3
Weight of weld metal/ft of 3/8 in fillet weld = (0.283 lb/in3) × (1.02 in3) = 0.2887 lb/ft
From the calculation below, we see that the travel speed for a one-pass, 3/8 in fillet weld would be 5.52 ipm, 11.03 ipm for a two-pass fillet weld, or 16.55 ipm for a three-pass weld.
Travel Speed Calculation
Travel speed = (deposition rate) × (# of passes)/5 × (weight of weld metal per foot {lb/ft}) =
Travel speed = {7.96 x 1} / {5 x 0.2887} = 5.52 ipm
CALCULATING WIRE-FEED SPEED WITH DEPOSITION RATE
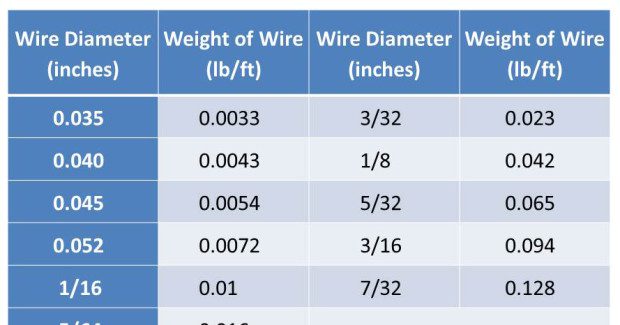
Let’s assume a requirement to make fillet welds at a rate of 12 lb/hr using 0.045 in welding wire. We can calculate the WFS using the formulas below and Weight of Weld Wire per foot in Table 1.
Wire-Feed Speed Calculation
Wire-feed Speed = (deposition rate)/5 × (weight of wire per foot {lb/ft}) = (12)/5 × (0.0054) = 444.4 ipm
Of course, the travel speed for a one-pass 3/8 in fillet weld at a 12 lb/hr deposition rate would be 8.31 ipm as calculated below:
Travel Speed = (deposition rate) × (# of passes)/5 × (weight of weld metal {lb./ft}) = (12) × (1)/5 × (0.2887) = 8.31 ipm
MAKING IT EASIER
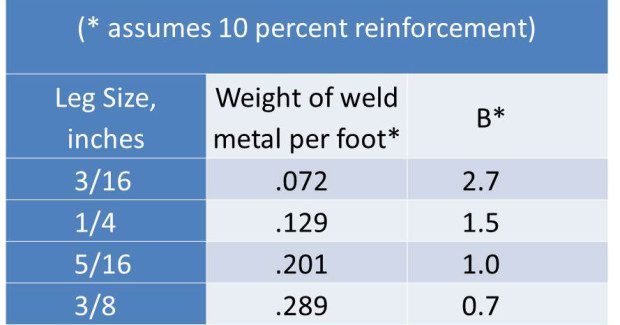
The Bartonian Conversion Factor (see Table 2) makes things a bit easier for fillet welds. The example below uses the conversion factor to calculate travel speed at 5.57 ipm for that same 3/8 in fillet weld using a 0.045 in solid wire.
Travel Speed = 7.96 × 0.7 = 5.57 ipm (.2887)
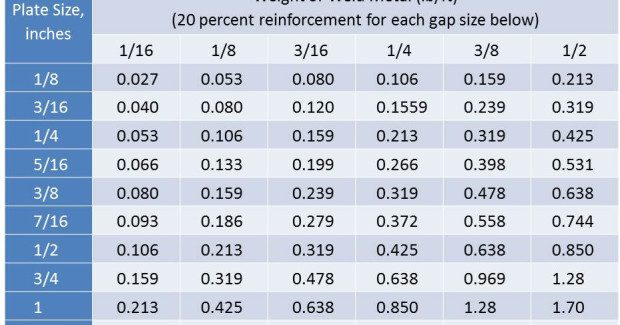
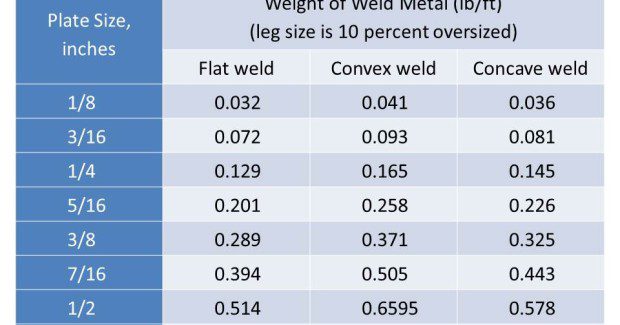
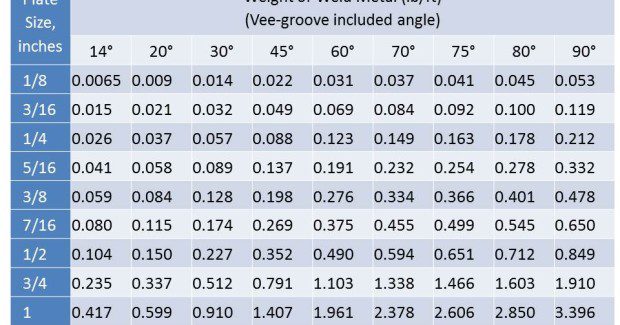
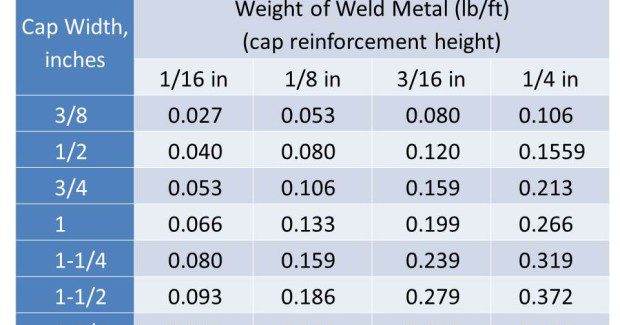
Weight of weld metal per foot can be calculated for any joint type by calculating the volume and multiplying by the density of the weld metal (eg. 0.283 lb/in3 for steel). However, the values shown in Table 3 through Table 6 eliminate the need to do the calculation. These values are taken from Table 12-1 in The Procedure Handbook of Arc Welding by the Lincoln Electric Co., and show the Weight of Weld Metal per Foot for several common joint types welded with steel. The following sample calculations use Tables 3 through 6.
SAMPLE CALCULATION NO.1
1/2 in plate Vee groove weld with 90 deg included angle and 1/8 in reinforcement using 0.052 in solid wire, 90%Ar/10%CO2 shielding gas. Manufacturer recommends WFS at 325 ipm and 30 volts.
Deposition Rate (lb/hr) = 13.1 × (0.052)2 × (325) × (1.0) = 11.51 lb/hr
Travel Speed for fill and cap passes = (11.51) × (6)/5 × (0.849 + 0.199) = 13.18 ipm
SAMPLE CALCULATION NO.2
3/8 in plate square butt weld into a backing, with a 3/16 in gap and 1/8 in reinforcement using 1/16 in cored wire, 75%Ar/25%CO2 shielding gas. Our process runs great with WFS at 285 ipm and 26 volts.
Deposition rate (lb./hr) = 13.1 × (1/16 in)2 × (285) × (.85) = 12.39 lb/hr
Travel speed for fill and cap passes = (12.39) × (1)/5 × (0.239 + 0.053) = 8.49 ipm
SAMPLE CALCULATION NO.3
What should my wire-feed speed be if I want to make a fat, 1/4 in fillet weld at 20 ipm travel speed using 0.045 in solid wire and 90%Ar/10%CO2 shielding gas?
Re-arranging the Travel Speed calculation above to solve for Deposition Rate we get:
Deposition rate = 5 × Travel speed × (Weight of weld metal {lb/ft})/(# of passes) = 5 × 20 ipm × (0.165)/1 = 16.5 lb/hr
Re-arranging the Deposition Rate calculation above to solve for Wire-feed Speed we get:
Wire-feed speed = Deposition rate/13.1 × (Wire diameter)2 × (Efficiency) = 16.5/13.1 × (.045 in.)2 × (1) = 622 ipm
SUMMARY
Using math and these simple formulas can reduce your weld-development time, and improve your pre-WPS documentation. These calculations will get you close, but some tweaking may have to be done to achieve your desired weld. Having a good starting point for welding procedure development will decrease time and guesswork on the shop floor.
Subscribe to learn the latest in manufacturing.